The $1 Unlimited Job Creation Program—a Mathematical Satire with Serious Implications
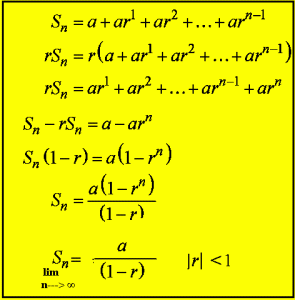
Massive quantitative easing is not necessary to stimulate any economy or to create hundreds of thousands, millions of jobs. The way to do this is as simple as spending $1.
Let’s say that President Obama or Ben Bernanke—actually anyone at all—steps into a shop and buys something for $1 and, in addition, informs the recipient that the $1 must be spent immediately—with nothing skimmed off as savings or withheld for later investment.
The recipient is further informed that the next recipient must be told and comply with the same instructions, under pain of very severe penalties.
That means immediate expenditure of that entire dollar on purchases that total $1—again, nothing skimmed off as savings or for later investment. The process is to be repeated and unbroken—like a sacred chain letter and game of “telephone”, but with no modification of the endlessly whispered, instantly forwarded message.
The Keynesian Multiplier
Those of you familiar with economics will see where this is going: This is the “Keynesian multiplier ”—the multiplication of wealth into a huge aggregate through dollar-denominated transactions unimpeded by any “marginal propensity to save”, all of this being a fancy way of saying that no portion of the next bit of income received, including by the next party in the next transaction, is withheld, instead with the entire amount being spent.
The math is pretty simple [but to be only skimmed here, if you hate math. You can jump to the boldfaced conclusion below, if you wish]: the total aggregate, national income generated by an infusion of money of any initial amount, “a”, after “n” transactions using it, is given by the formula shown: Sn= a [1-rn]/[1-r], where r=MPC, the “marginal propensity to consume”, i.e., the percentage of “a” consumed in a transaction and therefore passed on to the next recipient.
In this case, a= $1. So, things get even simpler as n gets bigger—much bigger, say, rapidly approaching infinity.
With infinity as the limit, S∞ = a/[1-r], if -1< r < 1.
But suppose 100% of that $1 is passed on in every transaction. That means that r = 1 and that the $1 generates another $1 that generates another $1 in income, ad infinitum.
In other mathematical terms, S∞= $1 + MPC + MPC2+ MPC4+….MPC∞= 1/[1-MPC].
If “1” is plugged into the main formula, for “a” and “r”, it becomes S∞ = 1/[1-1], or 1/0—which, technically is not allowed, since it is division by 0. However, it is a limit formula, so as n approaches, but does not reach infinity, the bottom bit, i.e., the denominator, becomes infinitesimally small, making S∞infinitely large.
If you appreciate common sense more than math, you’ll easily understand thatif every dollar spent is endlessly passed on for another purchase or payment, that single dollar will generate infinite income.
This is no joke. Both common sense and the formula are correct. Go ahead, test the formula: Suppose in each transaction, 10% of the initial $1 is withheld, e.g., as savings under a pillow. That means 90% will not. So, if that remaining 90 cents is passed on, the total income the initial $1 will generate will be $1/[$1-$0.9], i.e., $1/[$0.1], which is $10, including the original $1 that will generate another $9 in income. Strung out as a series of transactions, that looks like this: $1 + $0.90 + $0.81 + $0.729 +……..n∞= $10.
Quantitative Easing, or Teasing?
Now you can see the potential for Ben Bernanke’s $1 infusion into the economy and what an injection of, say, $1 trillion can accomplish, even with a substantial marginal savings rate.
Surely, if an infusion of $1 into the economy can generate infinite income, and that income is a measure of demand, then that $1 can generate infinite demand—which means demand for more labor, presumably human [unless there are also infinite gains in productivity per existing worker, making new hiring unnecessary or attractive].
This means more jobs—indeed, it means full employment.
So what’s the snag? The killer snag is that the $1 will generate infinite income, but only over [nearly] infinite transactions over—ouch—infinite time, assuming that each transaction takes time. The “velocity” of the money, i.e., the number of transactions per second, would have to be virtually infinitely large and $1 at a time, sequentially. This means virtually zero time per transaction.
This obstacle makes all the other theoretical considerations, such as how many jobs would actually be created by infinite aggregate income purely academic, since the key premise, that infinite income is generated, cannot hold.
One intriguingly anonymous analysis, prodigiously titled “Voodoo Economics, Part 1, The Keynesian Multiplier Demystified—The Faults and Fallacies behind the Idea of Benevolent Investment ”, offers a close and thought-provoking critique of what has been called the “Keynesian Multiplier Fallacy” and of the alleged efficacy of government cash infusions into the economy.
Agree with it or not, you’ll find it will make you think—very carefully.
But Wait!
But wait! There may be a way to implement the $1 unlimited job creation program: If somehow the transactions take virtually zero time, couldn’t a staggering amount of national income be generated very quickly, if not instantaneously? Might that not then translate into job growth?
Ah, there’s one more problem: What can you buy for exactly $1 these days, buy it instantaneously and buy it from someone who can repeat the process at the same blinding speed?
My best guess: Give the initial $1 to someone with a smart phone and instruct him or her to buy or sell you a phone app for a buck. Given how nimble the fingers of most smart phone owners are, that could be accomplished virtually instantaneously; and given how eager the app sellers are, the total time for the transaction might be very, very short, indeed.
Maybe even as short as the average compulsive texter’s attention span.

